Crypto #7: QKE
Vào một ngày đẹp trời, Alice và người tình của mình là Bob muốn hẹn hò với nhau, Alice muốn gửi một tin nhắn cho Bob, dưới dạng văn bản chứa thời gian và địa điểm đi chơi. Alice và Bob ở hai xóm khác nhau và họ phải nhắn tin qua Messenger hoặc điện thoại. Khổ nỗi, vợ của Bod - Eve giờ đây đã biết chồng mình ngoại tình và luôn theo dõi gắt gao mọi hành vi của anh ta, Alice không thể mã hóa thông điệp của mình vì Eve hoàn toàn có khả năng xâm nhập vào và nghe nội dung bất cứ lúc nào, Eve có thể lưu tin nhắn được mã hóa từ Alice và sẽ khám phá cơ chế mã hóa. Và dĩ nhiên Alice sẽ không dại gì mà sử dụng một giao thức đơn giản, cô phải sử dụng các giải pháp khác. Cơ hội nào để cuộc tình giữa Alice và Bob được tiếp diễn?
Để đối phó với Eve, Alice sử dụng một cơ chế mã hóa có tên OTP (One-Time-Pad) mà bản thân nó tạo ra bản mã không hề liên quan với tin nhắn gốc, tức là bản mã hoàn toàn là ngẫu nhiên.
Vì Alice và Bob đều trao đổi thông tin qua mạng máy tính nên nội dung tin nhắn sẽ là một chuỗi nhị phân 01 có chiều dài $n$. Alice tung một đồng xu $n$ lần sao cho độ dài bit khóa đúng bằng độ dài bit nội dung. Cô tạo ra một chuỗi các bit ngẫu nhiên do đó khóa của cô là khóa ngẫu nhiên và không ai có thể biết được (0 ngửa 1 sấp). Giả sử Alice và Bob có thoả thuận trước khóa với nhau, họ có thể trao đổi thông điệp như sau:
Bước 1. Alice thực hiện tính toán (bản gốc XOR khoá) (0 xor 0 = 1, 0 xor 1 = 1 và 1 xor 1 = 0)
Bước 2. Alice gửi qua cho Bob, Eve có thể kiểm tra tùy ý.
Bước 3. Bob lấy và tính theo cách tương tự sau khi Eve không còn nghi ngờ.
Tóm tắt lại giao thức này:

Thoạt đầu có vẻ hoàn hảo nhưng vẫn có vấn đề với việc Alice và Bob tiếp tục sử dụng giao thức này:
-
Phải có một khóa mới mỗi khi một tin nhắn được gửi đi. Nếu cùng một khóa sử dụng hai lần hoặc nhiều hơn, tin nhắn có thể bị phát hiện dễ dàng nếu phân tích thống kê, và đó là nguồn gốc sinh ra tên OTP.
-
Giao thức này chỉ an toàn khi Eve không biết khóa (nhớ, Alice và Bob phải chia sẻ cùng một pad để giao tiếp). Do đó sau mỗi lần gặp nhau 2 người chỉ nhắn được mỗi 1 tin.
Giao thức BB84: Giải pháp cứu cánh cho Alice
Trong khi xài OTP, Alice nhận ra rằng vấn đề phân phối khóa là vấn đề chính cần phải giải quyết, sử dụng mã RSA sẽ khắc phục nhưng thời gian rồi Eve cũng sẽ giải ra thừa số nguyên tố, vả lại Alice sẽ cực kỳ mệt mỏi nếu sử dụng nó. Do đó, cô tìm đến cách giải quyết vấn đề khác - một ý tưởng thông minh khai thác cơ học lượng tử. Ý tưởng này hình thành cơ sở của giao thức trao đổi khóa lượng tử (QKE) đầu tiên. Giao thức trao đổi khóa lượng tử đầu tiên được phát minh bởi Charles Bennett và Gilles Brassard vào năm 1984, và do đó có tên là BB84.
Đầu tiên hãy phân tích xem Eve có thể làm gì nếu cô ấy kiểm tra, hoặc nghe lén các bit (ta sẽ gọi đây là các bit cổ điển để phân biệt với bit lượng tử):
-
Cô ấy có thể tạo bản sao các phần tùy ý của luồng bit được mã hóa và lưu trữ chúng ở đâu đó để sử dụng trong phân tích và điều tra sau này.
-
Nếu Eve muốn tạo bằng chứng ngoại tình, cô ấy có thể nghe lén mà không ảnh hưởng đến luồng bit, tức là, dấu vết nghe lén không tồn tại.
Bây giờ, giả sử rằng Alice gửi qubit, thay vì bit.
Chuyện gì sẽ xảy ra?
-
Eve không thể tạo ra các bản sao hoàn hảo của luồng qubit bởi định lý không nhân bản ngăn điều này.
-
Hành động đo luồng qubit sẽ thay đổi qubit.
Lúc đầu, những điểm nêu trên dường như là những hạn chế, bởi vì đứng từ bên ngoài thì Eve lẫn Bob không khác gì nhau với vai trò là người nhận. Nhưng từ góc nhìn của Alice và Bob, nó hóa ra là những cơ hội tuyệt vời. Thế nghĩa là sao? Giả thuyết ở đây là định lý không nhân bản làm giảm khả năng sử dụng lại các thông điệp trong quá khứ của Eve. Quan trọng hơn, mỗi khi cô đo dòng qubit, sẽ gây ra sự suy sụp hàm sóng và làm rối loạn qubit, khiến Alice và Bob phát hiện cô đang nghe lén.
Mục tiêu của Alice là gửi cho Bob chìa khóa thông qua một kênh lượng tử. Cũng giống như trong giao thức One -Time - Pad, khóa của cô là một chuỗi các bit ngẫu nhiên (cổ điển) thu được bằng cách tung một đồng xu. Alice sẽ gửi một qubit mỗi lần. Cô sẽ gửi như thế nào?
Trong giao thức này, Alice sẽ sử dụng hai cơ sở trực giao khác nhau như sau:
|$+\rangle=($|$\rightarrow\rangle,$|$\uparrow \rangle)=([1, 0]^T,[0, 1]^T)$
và:
|$X\rangle=($|$\nwarrow\rangle,$|$\nearrow\rangle)=(\frac{1}{\sqrt{2}}[-1,1]^T,\frac{1}{\sqrt{2}}[1, 1]^T)$
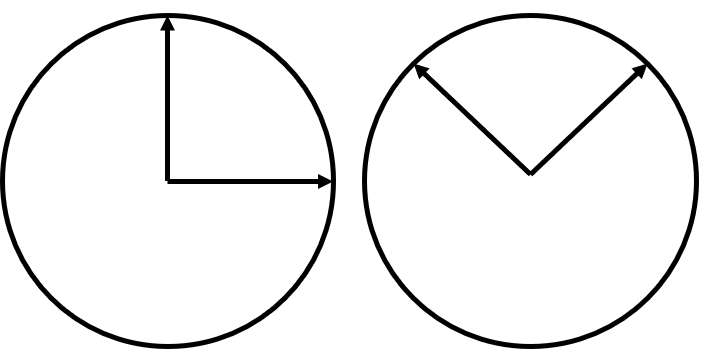
Chúng ta sẽ đề cập đến cơ sở đầu tiên là $+$ và thứ hai là $X$. Về cơ bản, chúng là hai đơn vị thay thế bit cổ điển mà Alice và Bob sẽ sử dụng để giao tiếp.
Trong 2 cơ sở này, trạng thái |$0\rangle$ và |$1\rangle$ được mô tả như sau:
| State | $+$ | $X$ |
|---|---|---|
| $|0\rangle$ | $|\rightarrow\rangle$ | $|\nearrow\rangle$ |
| $|1\rangle$ | $|\uparrow \rangle$ | $|\nwarrow\rangle$ |
Để tiện gọi thì ta sẽ kí hiệu góc cho 4 trạng thái trên, góc 0 là từ mũi tên nằm ngang và chiều dương ngược chiều kim đồng hồ.
Ví dụ, trong cơ sở $+$, trạng thái $0$ sẽ tương ứng với |$0\rangle$. Nếu Alice đang dùng cơ sở $X$ và muốn truyền đạt |$1\rangle$, cô ấy sẽ gửi qubit có trạng thái $135^{\circ}$. Tương tự, nếu Alice gửi $90^{\circ}$ và Bob đo lường được $90^{\circ}$ trong cơ sở $+$, anh ta phải ghi là |$1\rangle$.
Thực hiện điều trên sẽ không có vấn đề gì nếu đó là những trạng thái cơ bản, nhưng trạng thái chồng chất thì sao? Nếu Bob đo các photon bằng cách sử dụng cơ sở $+$, anh ta sẽ chỉ thấy các photon là $0^{\circ}$ hoặc $90^{\circ}$. Điều gì xảy ra nếu Alice gửi $45^{\circ}$ và Bob đo lường nó trong cơ sở $+$? Nó sẽ ở trạng thái chồng chất:
|$\nearrow\rangle=\frac{1}{\sqrt{2}}($|$\uparrow \rangle+$|$\rightarrow \rangle)$
Nói cách khác, sẽ có cơ hội 50 - 50 là Bob ghi là |$0\rangle$ hoặc |$1\rangle$ sau khi đo lường. Một lần nữa, Alice có thể sử dụng cơ sở $X$, dự định gửi |$0\rangle$, và Bob có 50% ghi |$1\rangle$ và 50% ghi |$0\rangle$. Trong tất cả các trường hợp thì có 4 trạng thái chồng chất khả dĩ:
|$\nwarrow\rangle$ khi đo lường trong $+$: $\frac{1}{\sqrt{2}}$|$(\uparrow \rangle-$|$\rightarrow \rangle)$
|$\nearrow\rangle$ khi đo lường trong $+$: $\frac{1}{\sqrt{2}}($|$\uparrow \rangle+$|$\rightarrow \rangle)$
|$\uparrow\rangle$ khi đo lường trong $X$: $\frac{1}{\sqrt{2}}($|$\nearrow \rangle+$|$\nwarrow \rangle)$
|$\downarrow\rangle$ khi đo lường trong $X$: $\frac{1}{\sqrt{2}}($|$\nearrow \rangle-$|$\nwarrow \rangle)$
Alice và Bob không cần xác định được thứ tự sử dụng của hai cơ sở, tuy nhiên họ vẫn sẵn sàng để bắt đầu giao tiếp. Dưới đây là các bước của giao thức:
Bước 1. Alice tung đồng xu $n$ lần để xác định bit cổ điển để gửi. Sau đó cô tung đồng xu $n$ lần khác để xác định cơ sở. Sau đó, cô gửi các bit theo cơ sở tương ứng. Ví dụ, nếu $n=12$, hoạt động của Alice sẽ được tóm tắt như thế này:
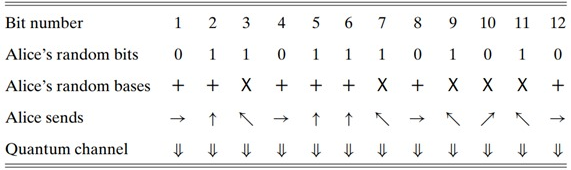
Bước 2. Khi chuỗi qubit đạt tới Bob, anh ta không biết cơ sở nào mà Alice sử dụng để gửi chúng, vì vậy để xác định cơ sở đo, anh ta cũng tung đồng xu $n$ lần. Sau đó tiếp tục đo lường qubit trong những cơ sở ngẫu nhiên đó. Trong ví dụ, tóm tắt hành động của Bob:
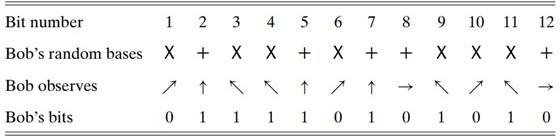
Đây là điều bất lợi: theo quy luật xác suất chỉ một nửa cơ sở của Bob giống Alice, trong trường hợp này kết quả của anh ta sau khi đo qubit sẽ giống hệt với bit ban đầu của Alice. Nửa còn lại, kết quả đo lường của Bob sẽ đúng khoảng 50%. Tức là tỉ lệ chính xác sẽ là $\frac{3}{4}$.
Chúng ta hãy tiếp tục với giao thức, xét trường hợp: Nếu Eve nghe lén thông tin mà Alice truyền và gửi thông tin giả mạo đó tới cho Bob.
Eve cũng không biết cơ sở Alice dùng để gửi mỗi qubit, vì vậy cô phải hành động như Bob. Cô ấy cũng sẽ tung đồng xu $n$ lần. Nếu tất cả cơ sở của Eve giống hệt với Alice, thì thông tin của cô ấy sẽ chính xác và thông tin giả mạo gửi cho Bob cũng sẽ chính xác. Mặt khác, nếu cơ sở của cô khác với Alice, bit của cô ấy sẽ chỉ có 50% đúng. Tuy nhiên, đây là điều khó khăn: qubit giờ đã sụp đổ thành một trong hai thành phần của cơ sở Eve. Bởi vì theo định lý không nhân bản, Eve không thể tạo ra bản sao của qubit ban đầu và sau đó gửi nó (sau cuộc thăm dò của cô ấy), cho nên cô ấy chỉ có thể gửi một qubit khác sau khi quan sát.
Do đó, nếu Eve chặn và đo từng qubit được gửi đi, cô sẽ gây ảnh hưởng đến cơ hội giống nhau giữa Alice và Bob.
Bằng cách tính toán một số thống kê đơn giản, hành động của Eve sẽ dễ dàng bị phát hiện. Sau khi Bob đã giải mã luồng qubit, anh ta có trong tay một chuỗi dài $n$. Bob và Alice sẽ thảo luận về các bit nào được gửi và nhận trong cùng một cơ sở. Họ có thể làm điều này công khai nếu Eve đang nghe lén hoặc sau khi Eve kiểm tra Bob.
Bước 3. Bob và Alice so sánh cơ sở mà họ sử dụng ở mỗi bước. Bob có thể nói với Alice là $X$, $+$, $X$, $X$, … Alice trả lời bằng cách nói với anh ta cái nào đúng, cái nào sai. Mỗi lần Bob không đúng, Alice và Bob sẽ loại bỏ ra bit tương ứng. Tiến hành theo cách này cho đến khi kết thúc, họ thu được một chuỗi các bit được gửi và nhận trong cùng một cơ sở. Nếu Eve không nghe lén, thì kết quả này phải giống hệt nhau và chuỗi sẽ có chiều dài $\frac{n}{2}$.
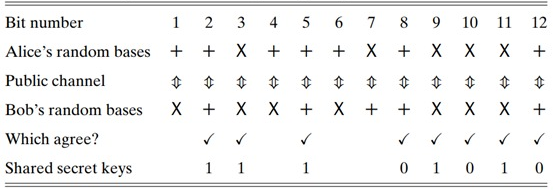
Nhưng nếu Eve đang nghe lén thì sao? Alice và Bob cũng muốn biết họ có an toàn hay không khi đang liên lạc nếu Eve (hay bất kỳ ai khác) đang nghe lén. Để thực hiện điều này, Họ so sánh một số bit trong phần tiếp theo.
Bước 4. Bob chọn ngẫu nhiên một nửa số bit nữa $\frac{n}{4}$ và công khai so sánh chúng với Alice. Nếu họ không đồng ý với nhau với hơn một tỷ lệ nhỏ (có thể do nhiễu), họ biết rằng Eve đang nghe lén và gửi thông tin giả mạo cho Bob. Trong trường hợp đó, họ phải thử một cách khác hoặc đợi dịp sau liên lạc. Nếu $\frac{n}{4}$ bit này là giống nhau, có nghĩa là Eve có khả năng tiên đoán tuyệt vời (this is impossible) hoặc không có ai nghe lén cả. Sau đó, họ chỉ đơn giản là xóa bỏ phần kiểm tra đã được tiết lộ và phần còn lại là khóa riêng bí mật chưa được tiết lộ.

Trong giao thức này, Bước 3 đã loại bỏ một nửa số qubit ban đầu được gửi đi. Vì vậy, nếu chúng ta bắt đầu với $n$ qubit, chỉ có $\frac{n}{2}$ qubit có sẵn sau Bước 3. Hơn nữa, Alice và Bob hiển thị công khai một nửa số qubit kết quả trong Bước 4. Điều này khiến họ chỉ có $\frac{n}{4}$ qubit so với bản gốc. Đừng lo lắng về điều này, vì Alice có thể làm cho dòng qubit của cô lớn hơn. Nếu Alice gửi một khóa $m$ bit, cô ấy chỉ đơn giản là gửi một luồng $4m$ qubit.
Giờ đây, Alice và Bob có thể rủ nhau đi chơi hay hẹn hò bất kỳ lúc nào họ thấy thích hợp, Eve đã hoàn toàn bất lực trước tình trạng này và cô ấy hay bất kỳ ai khác cũng sẽ chẳng có chứng cứ để đưa Bob ra đường. Nếu Eve làm được điều đó thì có nghĩa là một trọng những điều cốt lõi của cơ học lượng tử là sai, mà khi điều cốt lõi là sai thì có lẽ toàn bộ cơ học lượng tử cũng sai nốt. Và khi đó thì các nhà khoa học lại phải điên đầu tìm ra một nền tảng lý thuyết mới.
Kết thúc bài 7, bài viết tham khảo cuốn sách Quantum Computing for Computer Scientists (tác giả Noson S Yanofsky và Micro A Mannucci)
Bài viết gốc: Spiderum
Tác giả
Vũ Tuấn Hải - Monadotory