Haskell #5: Curry

Haskell #4: Đệ quy

Qua những chương đầu tiên, những ai đã quen với lập trình từ trước có lẽ sẽ hiểu vấn đề và những ý tưởng tôi truyền tải một cách nhanh chóng, tuy nhiên Haskell không hoàn toàn dễ như bạn tưởng. Bài viết sau đây mới thực sự là khởi đầu.

Higher order function

Những cao thủ thi đấu lập trình sử dụng C++ chắc chắn đã biết tới con trỏ hàm - một khái niệm giúp cho chúng ta có thể truyền hàm vào hàm dưới dạng tham số, hoặc trả về hàm sau khi thực thi hàm nào đó - cú pháp này giúp cho C++ không cần dùng tới những Design Pattern như Factory, Builder, … vốn sinh ra do giới hạn của những ngôn ngữ thuần OOP như Java, C#, …

Tuy con trỏ hàm giúp C++ loại bỏ quá trình sinh ra các class (nếu cần thực hiện chức năng nào đó giống Design Pattern 00P) nhưng cú pháp của chúng vẫn khá loằng ngoằng. Ví dụ như sau:

void swapValue(int &value1, int &value2) 
{
	...
}

int main()
{
	void(*pSwap) (int &, int &) = swapValue;
	...
}

Điều này trong Haskell được xử lý như thế nào?

Nếu chúng ta khái quát hóa khái niệm hàm, thì rõ ràng tham số truyền vào có thể là hàm và giá trị trả về cũng có thể là hàm. Đối với hàm $f$ được truyền vào hoặc được nhả ra từ hàm $g$, ta nói răng $f$ có bậc thấp hơn $g$ hay ngược lại, $g$ có bậc cao hơn $f$. Hàm bậc cao không chỉ là vấn đề quan trọng trong Haskell, mà còn có thể nói là thước đo kinh nghiệm trong việc dùng ngôn ngữ này. Chúng là công cụ mạnh giúp ta giải quyết bài toán và suy tư. Sau này, bạn sẽ gặp nhiều trường hợp, trong đó nếu không sử dụng khái niệm hàm bậc cao thì code sẽ khó hiểu và khá dài dòng.

Hàm Curry

Trong Haskell, các bác nhà ta định nghĩa rằng mỗi hàm chỉ nhận duy nhất một tham số. Nếu hàm cần nhiều tham số, chúng ta có một khái niệm quan trọng cần ghi nhớ là hàm Curry (curried function). Đó là cái gì?

image info

Curry function tồn tại xung quanh con người nhưng có lẽ không ai để ý. Ví dụ về việc rút tiền trong ATM, thường thì chúng ta sẽ làm 3 bước: đút thẻ, nhập mã PIN và chọn số tiền. Như vậy ATM thực chất là hàm $f$ nhận vào 3 tham số (thẻ, mã PIN, số tiền) và trả về tiền, nhưng bạn có thể thấy rằng chúng ta không thể nạp 3 tham số trên vào máy cùng một lúc mà phải nạp từng cái một và chờ phản hồi.

Bước 1, khi nạp thẻ, $f$ không trả về tiền ngay mà trả về hàm $f_1$, hàm này có thể nhận vào một tham số (mã PIN) và trả về $f_2$.

Bước 2, chúng ta nhập mã PIN vào $f_1$ (vì ATM chỉ trả về $f_1$), $f_1$ trả về hàm $f_2$, hàm này có thể nhận vào một tham số (số tiền) và trả về tiền thật. Dễ nhận ra rằng $f_2$ chính là hàm cổ điển (không có yếu tố curry).

Quan sát kĩ bạn sẽ nhận ra rằng $f_1$, $f_2$ là những hàm độc lập nhưng nằm trong quy trình xử lý của $f$. Nếu biểu diễn bằng toán học (Giải tích lambda), chúng ta sẽ có biểu thức sau.

Hàm gốc $f: (Card \times PIN \times Amount) \rightarrow Money$.

Hàm Curry $f: Card\rightarrow (PIN\rightarrow( Amount \rightarrow Money))$ trong đó $f_1: PIN\rightarrow (Amount \rightarrow Money)$, $f_2: Amount \rightarrow Money$.

Vì các dấu ngoặc theo quy luật và cũng khá vướng víu nên chúng ta có thể bỏ luôn:

$f: Card\rightarrow PIN\rightarrow Amount \rightarrow Money$

Một ví dụ thân thuộc là hàm max, nó nhận hai tham số rồi trả về số lớn hơn. Nếu gọi max 4 5, thoạt đầu có thể bạn nghĩ rằng câu lệnh trên đơn giản là truyền 4 và 5 vào hàm và cho nó thực thi nhưng thực ra ta đã tiến hành tới tận hai bước. Bước một là tạo ra hàm $f_1$ nhận tham số 4 ($f_1$ trả về $f_2$, $f_2$ là hàm nhận vào một tham số nữa và so sánh với tham số của $f_1$).

ghci> max 4 5
5
ghci> (max 4) 5
5

Kiểu của max là max :: (Ord a) => a -> a -> a. Cũng có thể viết dưới dạng max :: (Ord a) => a -> (a -> a). Nếu biểu đạt bằng lời: max nhận vào một đối tượng a rồi trả về (dấu -> là ký hiệu cho “trả về”) một hàm, hàm này cũng nhận một đối tượng kiểu a rồi trả về đối tượng cùng kiểu. Đó là lý do tại sao kiểu trả về cũng như tham số của hàm chỉ đơn giản được ngăn cách bởi dấu mũi tên.

Dấu cách giữa (max 4) và 5 chính là lời gọi hàm. Đây là là toán tử có độ ưu tiên cao nhất.

Vậy thì điều này có gì lợi cho ta? Nói nôm na, nếu ta gọi một hàm mà đưa thiếu tham số, ta sẽ thu được một hàm áp dụng từng phần (partially applied), nghĩa là một hàm nhận vào tất cả bao nhiêu tham số mà ta để thừa lại. Bằng cách áp dụng từng phần (gọi hàm với ít tham số, nếu bạn muốn) bạn có thể tiện tay tạo ra các hàm mỗi khi cần đến, ta có thể truyền chúng vào các hàm khác hoặc ghép dữ liệu với chúng.

Hãy xem hàm đơn giản sau đây:

multThree :: (Num a) => a -> a -> a -> a
multThree x y z = x * y * z
ghci> multThree 3 5 9

Trước tiên, 3 được áp dụng cho multThree, vì chúng được ngăn giữa bởi một dấu cách. Kết quả là tạo ra hàm $f_1$ ($f_1$ nhận một tham số rồi trả về một hàm khác). Khi gọi $f_1$ với tham số 5 chúng ta nhận được $f_2$, $f_2$ nhận một tham số và trả về tích của tham số đó với 15, cuối cùng thu được 135. Hãy nhớ rằng type signature của multThree cũng có thể viết là multThree :: (Num a) => a -> (a -> (a -> a)). Thứ đứng đằng trước dấu -> là tham số mà hàm nhận vào và đứng đằng sau là đối tượng trả về.

Vì vậy multThree có thể nhận một a rồi trả về đối tượng kiểu (Num a) => a -> (a -> a). Tương tự, đối tượng (hàm) này nhận vào một a rồi trả về một hàm có kiểu (Num a) => a -> a. Và hàm này, cuối cùng, sẽ chỉ nhận một a và trả về một a. Ví dụ về công dụng của lời giải thích trên:

ghci> let multTwoWithNine = multThree 9
ghci> multTwoWithNine 2 3
54
ghci> let multWithEighteen = multTwoWithNine 2
ghci> multWithEighteen 10
180

Nếu gọi hàm và đưa thiếu tham số, ta sẽ tạo ra hàm mới. Ví dụ, hàm nhận vào một số rồi so sánh nó với 100?

compareWithHundred :: (Num a, Ord a) => a -> Ordering
compareWithHundred x = compare 100 x

Nếu ta gọi nó với 99, nó sẽ trả về GT. Đơn giản. Lưu ý rằng x đứng bên phải trong cả hai vế của phương trình. Nếu chỉ đơn thuần gọi compare 100, nó sẽ trả về một hàm mà hàm này nhận vào một con số rồi so sánh số đó với 100. Ta có thể viết lại như sau:

compareWithHundred :: (Num a, Ord a) => a -> Ordering
compareWithHundred = compare 100

Type signature vẫn giữ nguyên, vì compare 100 trả về hàm. Hàm compare có kiểu (Ord a) => a -> (a -> Ordering) và khi được gọi với 100 thì trả về ` (Num a, Ord a) => a -> Ordering`. Ràng buộc về lớp xuất hiện ở đây vì 100 cũng thuộc về lớp Num.

Hãy chắc chắn rằng bạn hiểu được cách hoạt động của hàm curry và áp dụng từng phần vì chúng rất quan trọng trong sau này.

Các hàm trung tố cũng có thể được áp dụng từng phần bằng cách dùng cú pháp section. Để cắt một hàm trung tố, ta sẽ kẹp chúng giữa cặp ngoặc đơn. Bằng cách này ta sẽ tạo ra hàm nhận vào một tham số rồi sau đó áp dụng cho vế đang bị thiếu. Một ví dụ như sau:

divideByTen :: (Floating a) => a -> a
divideByTen = (/10)

Việc gọi, chẳng hạn, divideByTen 200 tương đương với việc viết 200 / 10, và cũng giống như (/10) 200.

Một hàm có nhiệm vụ kiểm tra xem ký tự nhập vào có phải là chữ cái viết in hay không:

isUpperAlphanum :: Char -> Bool
isUpperAlphanum = (`elem` ['A'..'Z'])

Ngoại lệ duy nhất khi dùng section là việc dùng -. Theo định nghĩa section thì lẽ ra (-4) sẽ tạo ra hàm để nhận một tham số rồi trừ đi 4. Tuy nhiên, để cho tiện, (-4) có nghĩa là âm 4 (chúng ta có thể thay thế bằng hàm subtract):

(subtract 4)

Một lưu ý khác là khi chúng ta cố gắng in một hàm lên cửa sổ console, chẳng hạn multThree 3 4 trong GHCI (thay vì gán nó bằng let hay truyền vào một hàm khác).

ghci> multThree 3 4
<interactive>:0:1: error:
    * No instance for (Show (Integer -> Integer))
        arising from a use of `print'
        (maybe you haven't applied a function to enough arguments?)
    * In a stmt of an interactive GHCi command: print it

GHCI báo cho ta biết rằng biểu thức vừa nhập đã tạo ra một hàm có kiểu a -> a nhưng không biết làm thế nào để in nó ra màn hình. Hàm không thuộc lớp Show nên ta không thể nhận được string để in hàm ra màn hình. Còn khi ta gõ, chắng hạn như, 1 + 1 từ GHCI prompt, ban đầu nó sẽ tính được 2 rồi gọi show đối với 2 để thu được một dạng hiển thị số đó. Và dạng hiển thị của 2 chính là chuỗi “2”, và nó sẽ được in ra màn hình cho chúng ta thấy.

Hàm bậc cao

Hàm có thể nhận hàm khác làm tham số rồi trả về hàm. Để minh họa điều này, ta sẽ tạo một hàm, hàm này nhận vào một hàm rồi áp dụng nó hai lần cho một đối tượng nào đó!

applyTwice :: (a -> a) -> a -> a
applyTwice f x = f (f x)

Trước tiên, hãy lưu ý type signature. Trước đây, chúng ta có thể loại bỏ cặp ngoặc đơn giữa các tham số và đối tượng trả về. Còn bây giờ, ngoặc đơn là bắt buộc; để chỉ rằng tham số thứ nhất là hàm nhận vào một thứ gì đó rồi trả về cũng thứ đó. Tham số thứ hai cùng kiểu, và giá trị trả về cũng cùng kiểu. Ta có thể đọc type signature này theo cách curry, nhưng để tránh nhức đầu có thể đơn giản hóa rằng applyTwice nhận vào hai tham số rồi trả về một thứ. Tham số đầu tiên là một hàm (có kiểu a -> a) và tham số thứ hai cũng là a. Hàm này có thể là Int -> Int hay String -> String hoặc thế nào cũng được, nhưng tham số thứ hai phải cùng kiểu.

Lưu ý: Từ nay trở đi, ta sẽ nói rằng các hàm nhận nhiều tham số mặc dù mỗi hàm thật ra chỉ nhận một tham số rồi trả về một hàm áp dụng từng phần cho tới khi có một hàm trả về một giá trị cụ thể. Vì vậy, để đơn giản, ta sẽ nói rằng a -> a -> a nhận vào hai tham số, mặc dù ta đã biết rằng bên trong nó đang diễn ra chuyện gì.

ghci> applyTwice (+3) 10
16
ghci> applyTwice (++ " HAHA") "HEY"
"HEY HAHA HAHA"
ghci> applyTwice ("HAHA " ++) "HEY"
"HAHA HAHA HEY"
ghci> applyTwice (multThree 2 2) 9
144
ghci> applyTwice (3:) [1]
[3,3,1]

Sự kì diệu và tiện dụng của áp dụng hàm từng phần đã rõ ràng. Nếu hàm được viết yêu cầu chúng ta trả về một hàm chỉ nhận một tham số, thì ta có thể đơn giản là áp dụng từng phần đến khi nó chỉ còn nhận một tham số, rồi truyền hàm này đi.

Bây giờ ta sẽ áp dụng hàm bậc cao để tạo ra hàm zipWith. Hàm này nhận vào các tham số gồm có một hàm và hai List rồi nối hai List lại bằng cách áp dụng hàm giữa hai phần tử có thứ tự tương ứng. Sau đây là cách ta lập nó:

zipWith' :: (a -> b -> c) -> [a] -> [b] -> [c]
zipWith' _ [] _ = []
zipWith' _ _ [] = []
zipWith' f (x:xs) (y:ys) = f x y : zipWith' f xs ys

Hãy nhìn vào type signature. Tham số thứ nhất là một hàm nhận vào hai đối tượng và trả về một đối tượng thứ ba. Chúng có thể cùng kiểu với nhau. Tham số thứ hai và thứ ba đều là List. Kết quả cũng là một List. Cả ba List có thể có 3 kiểu khác nhau. Nếu type signature của hàm nói rằng nó chấp nhận một hàm a -> b -> c làm tham số, thì nó cũng sẽ chấp nhận type a -> a -> a, nhưng ngược lại thì không! Hãy nhớ rằng khi bạn code hàm bậc cao mà chưa cảm thấy chắc chắn về type, thì bạn có thể không khai báo type signature rồi kiểm tra xem Haskell suy luận nó thế nào bằng cách dùng :t.

Hàm này khá giống với hàm zip thông thường. Điều kiện biên vẫn y vậy, chỉ khác là có thêm một đối số (hàm nối), nhưng đối số đó không có ý nghĩa trong điều kiện biên, vì vậy ta chỉ cần dùng dấu _ để kí hiệu. Và phần thân hàm cũng tương tự zip, song nó không phải (x,y), mà là f x y. Một hàm bậc cao có thể được dùng cho một loạt những nhiệm vụ khác nhau nếu nó đủ độ tổng quát. Sau đây là màn biểu diễn cho thấy tất cả những việc mà hàm zipWith' có thể thực thi:

ghci> zipWith' (+) [4,2,5,6] [2,6,2,3]
[6,8,7,9]
ghci> zipWith' max [6,3,2,1] [7,3,1,5]
[7,3,2,5]
ghci> zipWith' (++) ["foo ", "bar ", "baz "] ["fighters", "hoppers", "aldrin"]
["foo fighters","bar hoppers","baz aldrin"]
ghci> zipWith' (*) (replicate 5 2) [1..]
[2,4,6,8,10]
ghci> zipWith' (zipWith' (*)) [[1,2,3],[3,5,6],[2,3,4]] [[3,2,2],[3,4,5],[5,4,3]]
[[3,4,6],[9,20,30],[10,12,12]]

Ta sẽ code một hàm khác đã có sẵn trong thư viện chuẩn, hàm flip. Flip đơn giản là nhận vào một hàm rồi trả về một hàm mới giống như hàm ban đầu, chỉ khác là hai đối số đã bị đổi chỗ. Ta có thể code nó như sau:

flip' :: (a -> b -> c) -> (b -> a -> c)
flip' f = g
    where g x y = f y x

Dựa vào type signature, ta nói rằng nó nhận một hàm, hàm này nhận a và b rồi trả về một hàm nhận b và a. Nhưng vì các hàm mặc định là curry, nên cặp ngoặc tròn thứ hai thực sự không cần thiết, vì -> mặc định là gắn với đối tượng bên phải nó. (a -> b -> c) -> (b -> a -> c) cũng giống như (a -> b -> c) -> (b -> (a -> c)), và cũng giống như (a -> b -> c) -> b -> a -> c. Ta đã viết là g x y = f y x. Nếu điều này đúng, thì f y x = g x y cũng đúng, phải vậy không nhỉ? Ghi nhớ điều đó, ta có thể định nghĩa hàm này đơn giản hơn.

flip' :: (a -> b -> c) -> b -> a -> c
flip' f y x = f x y

Ở đây, ta tận dụng được đặc điểm curry của hàm. Khi ta gọi flip’ f không có tham số y và x, nó sẽ trả về một f nhận vào hai tham số, nhưng gọi các tham số này theo thứ tự ngược lại. Mặc dù các hàm đã flip thường được truyền vào các hàm khác, ta vẫn có thể tận dụng curry khi code hàm bậc cao bằng cách nghĩ trước và viết ra kết quả sau cùng sẽ là gì nếu như hàm được gọi.

ghci> flip' zip [1,2,3,4,5] "hello"
[('h',1),('e',2),('l',3),('l',4),('o',5)]
ghci> zipWith (flip' div) [2,2..] [10,8,6,4,2]
[5,4,3,2,1]

Map & Filter

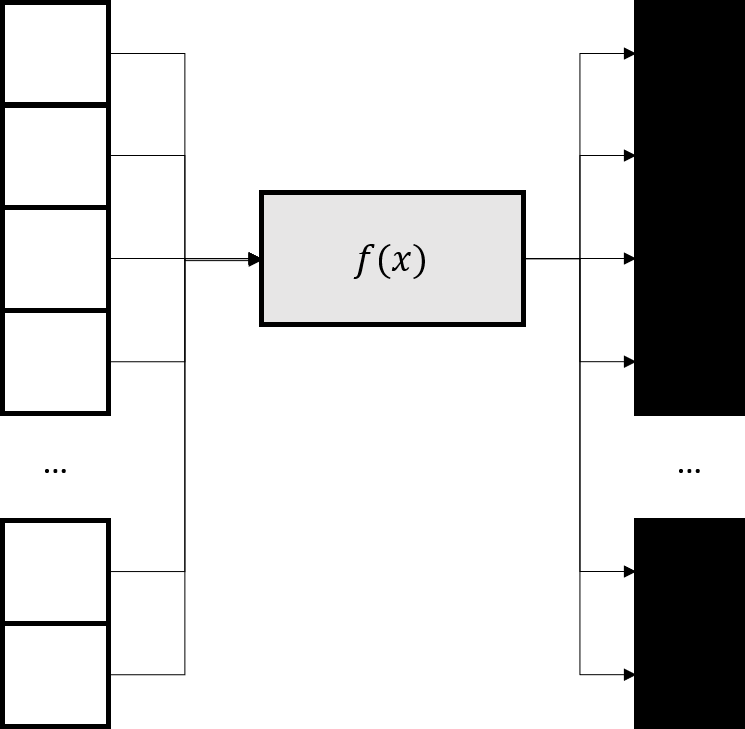
image info

Map nhận vào hàm và List rồi áp dụng hàm đó lên từng phần tử thuộc List, để tạo ra List mới. Ta hãy xem type signature của map là gì và nó được định nghĩa thế nào.

map :: (a -> b) -> [a] -> [b]
map _ [] = []
map f (x:xs) = f x : map f xs

Type signature nói rằng nó nhận vào một hàm, hàm này nhận a và trả về b, cùng List a, rồi trả về List b. Điều hay là chỉ cần nhìn vào type signature kiểu hàm, đôi khi bạn có thể nói được rằng nó làm gì. map là một trong số các hàm bậc cao đa năng. Nó có thể được dùng theo muôn vàn những cách khác nhau. Sau đây là màn trình diễn của hàm này:

ghci> map (+3) [1,5,3,1,6]
[4,8,6,4,9]
ghci> map (++ "!") ["BIFF", "BANG", "POW"]
["BIFF!","BANG!","POW!"]
ghci> map (replicate 3) [3..6]
[[3,3,3],[4,4,4],[5,5,5],[6,6,6]]
ghci> map (map (^2)) [[1,2],[3,4,5,6],[7,8]]
[[1,4],[9,16,25,36],[49,64]]
ghci> map fst [(1,2),(3,5),(6,3),(2,6),(2,5)]
[1,3,6,2,2]

Có thể bạn đã nhận ra mỗi phép tính này có thể thực thi được List comprehension. map (+3) [1,5,3,1,6] cũng giống như [x + 3 | x <- [1,5,3,1,6]]. Tuy nhiên, dùng map thì dễ đọc hơn trong trường hợp bạn chỉ áp dụng một hàm, đặc biệt khi bạn phải tính map của map, nếu viết List comprehension thì có quá nhiều ngoặc vuông.

image info

Filter là hàm nhận vào vị ngữ (hàm có nhiệm vụ thông báo điều gì đó là đúng hay sai, trong trường hợp này là hàm trả về boolean) và List rồi trả về List chỉ chứa các phần tử thỏa mãn vị ngữ này. Type signature như sau:

filter :: (a -> Bool) -> [a] -> [a]
filter _ [] = []
filter p (x:xs) 
    | p x       = x : filter p xs
    | otherwise = filter p xs

Khá đơn giản. Nếu p x trả về True, thì phần tử sẽ có mặt trong List mới. Một vài ví dụ sử dụng:

ghci> filter (>3) [1,5,3,2,1,6,4,3,2,1]
[5,6,4]
ghci> filter (==3) [1,2,3,4,5]
[3]
ghci> filter even [1..10]
[2,4,6,8,10]
ghci> let notNull x = not (null x) in filter notNull [[1,2,3],[],[3,4,5],[2,2],[],[],[]]
[[1,2,3],[3,4,5],[2,2]]
ghci> filter (`elem` ['a'..'z']) "u LaUgH aT mE BeCaUsE I aM diFfeRent"
"uagameasadifeent"
ghci> filter (`elem` ['A'..'Z']) "i lauGh At You BecAuse u r aLL the Same"
"GAYBALLS"

Tất cả những điều này đều có thể làm bằng List comprehension có sử dụng vị ngữ. Chẳng có quy định cứng nhắc buộc bạn khi nào phải dùng map và filter thay vì List comprehension, bạn tự quyết định cách nào dễ đọc hơn tùy vào code và hoàn cảnh cụ thể. Cách dùng filter nhiều lần tương đương với việc đưa nhiều vị ngữ vào trong List comprehension và các vị ngữ được liên kết với nhau bằng hàm logic &&.

Bạn còn nhớ hàm quicksort từ chương trước chứ? Ta đã dùng List comprehension để filter các phần tử nhỏ hơn (hoặc bằng), và các phần tử lớn hơn pivot. Ta có thể thực thi điều này với cách viết code dễ đọc hơn bằng filter:

quicksort :: (Ord a) => [a] -> [a]  
quicksort [] = []  
quicksort (x:xs) =   
    let smallerSorted = quicksort (filter (<=x) xs)
        biggerSorted = quicksort (filter (>x) xs) 
    in  smallerSorted ++ [x] ++ biggerSorted

Map và filter là nguyên liệu cốt yếu trong tay người lập trình hàm. Hãy nhớ lại cách ta giải bài toán tìm những tam giác vuông với chu vi cho trước. Nếu lập trình mệnh lệnh, ta có thể giải bằng cách lồng ba vòng lặp rồi kiểm tra xem tổ hợp ba cạnh hiện thời có thỏa mãn điều kiện tam giác vuông và với chu vi hay không. Nếu thỏa mãn, ta đã in kết quả ra màn hình hoặc lưu vào nơi khác. Trong lập trình hàm, bài toán đó có thể thực thi với map và filter. Bạn tạo ra một hàm nhận vào một giá trị rồi trả về kết quả nào đó. Ta map hàm này lên List rồi filter List cần tìm từ những kết quả thỏa mãn yêu cầu. Nhờ lazy evaluation của Haskell, ngay cả khi bạn map thứ gì lên List nhiều lần và filter nó nhiều lần, nó cũng chỉ duyệt qua List đúng một lần.

Ví dụ tìm $x_{max}:=maximum{x\in N, x < 100000, x\;\vdots \;3829}$. Để làm điều này, ta chỉ cần filter List.

largestDivisible :: (Integral a) => a
largestDivisible = head (filter p [100000,99999..])
    where p x = x `mod` 3829 == 0

Trước hết, ta tạo List chứa tất cả số dưới 100000 theo chiều giảm dần. Sau đó ta filter List này bằng vị ngữ thích hợp. Vì các số đã được xếp giảm dần, nên số đầu tiên thỏa vị ngữ sẽ là phần tử thứ nhất trong List sau khi filter. Ta không cần dùng List hữu hạn vì đã có lazy evaluation, ta chỉ lấy head của List sau khi filter, nên không cần bận tâm List đó là hữu hạn hay vô hạn. Evaluation kết thúc khi tìm được nghiệm.

Tiếp theo, ta sẽ tìm tổng của tất cả bình phương lẻ nhỏ hơn 10. Trước hết, vì sẽ dùng nó trong lời giải, nên ta sẽ dùng hàm takeWhile. Hàm này nhận vào vị ngữ và List rồi duyệt từ đầu List, trả về những phần tử thỏa vị ngữ. Khi tới phần tử không thỏa vị ngữ thì hàm sẽ dừng lại. Nếu ta muốn lấy từ đầu tiên của chuỗi "elephants know how to party", ta có thể viết takeWhile (/=' ') "elephants know how to party" và nó sẽ trả về "elephants". Được rồi. Tổng của tất cả những bình phương nhỏ hơn 100 và là số lẻ.

Trước hết, ta map hàm (^2) lên List vô hạn [1..]. Sau đó ta filter chúng để lấy số lẻ. Tiếp theo ta tiếp tục lấy những phần tử từ List cho đến khi chúng nhỏ hơn 100. Cuối cùng, ta tính tổng của List đó. Thậm chí ta còn không phải định nghĩa một hàm cho toàn bộ công việc này, ta có thể gõ dòng lệnh rồi chạy trực tiếp trong GHCI:

ghci> sum (takeWhile (<10) (filter odd (map (^2) [1..])))
10

Tuyệt vời! Bắt đầu bằng một số liệu ban đầu nào đó (List vô hạn chứa tất cả những số tự nhiên), ta map, filter rồi cắt bớt cho đến khi được List như ý, tiếp theo chỉ cần lấy tổng. Ta cũng đã có thể viết bằng List comprehension:

ghci> sum (takeWhile (< 10) [n ^ 2 | n <- [1..], odd (n ^ 2)])
10

Việc chọn cách nào đẹp hơn chỉ là vấn đề cá nhân. Ta có thể map và filter List vô hạn, vì thật ra nó không map và filter ngay. Chỉ khi ta buộc Haskell phải tính tổng thì hàm sum mới báo cho hàm takeWhile rằng nó cần những con số đó. takeWhile lại ép filter và map phải tiến hành.

Ở bài toán tiếp theo, ta sẽ tính chuỗi Collatz. Ta nhận vào một số tự nhiên. Nếu nó chẵn, hãy chia cho 2. Nếu lẻ, hãy nhân 3 rồi cộng với 1. Đem số thu được và áp dụng lại cách tính như trên, rồi cứ tiếp tục như vậy. Tóm lại, ta sẽ được một dãy số. Người ta cho rằng dù bắt đầu với con số nào, chuỗi cũng sẽ hội tụ về 1. Vì vậy, nếu ta bắt đầu bằng số 13, thì sẽ thu được dãy sau: [13, 40, 20, 10, 5, 16, 8, 4, 2, 1]. 13 * 3 + 1 bằng 40. 40 chia 2 bằng 20, … Ta thấy rằng chuỗi này có 10 số.

Bây giờ điều ta muốn biết như sau: với tất cả các số từ 1 đến 100, có bao nhiêu dãy số được tạo ra có độ dài hơn 15? Đầu tiên, ta hãy viết một hàm để tạo dãy số:

chain :: (Integral a) => a -> [a]
chain 1 = [1]
chain n
    | even n =  n:chain (n `div` 2)
    | odd n  =  n:chain (n*3 + 1)

Vì dãy kết thúc bằng 1, nên đó là điều kiện biên. Đây là một hàm đệ quy khá chuẩn mực.

ghci> chain 10
[10,5,16,8,4,2,1]
ghci> chain 1
[1]
ghci> chain 30
[30,15,46,23,70,35,106,53,160,80,40,20,10,5,16,8,4,2,1]

A! Dường như nó hoạt động tốt. Và bây giờ, hàm sau sẽ trả lời ta câu hỏi vừa rồi:

numLongChains :: Int
numLongChains = length (filter isLong (map chain [1..100]))
    where isLong xs = length xs > 15

Ta map hàm chain lên List [1..100] để thu được List các List. Sau đó, ta filter chúng bằng một vị ngữ để kiểm tra xem length có hơn 15 hay không. Một khi ta đã filter xong, ta sẽ tìm số List còn lại trong List kết quả. Lưu ý: Hàm này có kiểu là numLongChains :: Int vì length trả về một Int chứ không phải một Num a, điều này có lý do từ quá khứ. Nếu bạn muốn trả về một Num a là dạng tổng quát hơn, ta có thể áp dụng fromIntegral lên length thu được.

Dùng map, ta có thể làm được những việc như map (*) [0..], nếu không cần những lý do khác ngoài minh họa cách hoạt động của curry và cách các hàm (áp dụng từng phần) cũng được truyền như giá trị vào các hàm khác, hoặc đưa vào List (bạn chỉ không thể biến chúng thành string). Đến giờ, ta mới chỉ map các hàm nhận một tham số lên List, như map (*2) [0..] để thu được một List có kiểu (Num a) => [a], nhưng ta vẫn có thể viết map (*) [0..] mà không gặp phải vấn đề gì. Điều xảy ra ở đây là phần tử trong List được áp dụng vào hàm *, có kiểu (Num a) => a -> a -> a. Việc chỉ áp dụng duy nhất một tham số cho hàm nhận hai tham số sẽ trả về một hàm nhận một tham số. Nếu ta map * lên List [0..], ta sẽ thu về List các hàm chỉ nhận một tham số, vì vậy (Num a) => [a -> a]. map (*) [0..] tạo ra một List kiểu [(0*),(1*),(2*),(3*),(4*),(5*),…

ghci> let ListOfFuns = map (*) [0..]
ghci> (ListOfFuns !! 4) 5
20

Lưu ý rằng hàm !! sẽ lấy phần tử có chỉ số 4 từ List, tương đương việc ta thu được hàm (4*).

Kết thúc bài 5

Haskell #6: Lambda