Haskell #6: Lambda

Haskell #5: Hàm Curry

Lambda

Lambda $(\lambda)$ là tên gọi để chỉ các hàm vô danh xuất phát từ giải tích Lambda, chúng là cú pháp thuận tiện khi chúng ta cần dùng một hàm nào đó rồi bỏ ngay (giống như khăn giấy, dùng một lần sẽ bỏ đi).

Thông thường, lambda sẽ được tạo ra với mục đích truyền vào hàm bậc cao hơn. Để tạo lambda, ta sử dụng dấu \ (vì trông gần giống lambda $(\lambda)$ trong tiếng Hy Lạp) tiếp theo là các tham số, được ngăn bởi dấu cách. Sau đó là dấu -> rồi phần thân hàm. Ta thường bao chúng trong cặp ngoặc tròn, nếu không các hàm lambda sẽ kéo dài sang phải cho đến hết dòng.

Ở phần trước, chúng ta có hàm sau:

numLongChains :: Int
numLongChains = length (filter isLong (map chain [1..100]))
    where isLong xs = length xs > 15

Dễ thấy rằng ta đã gắn where trong hàm numLongChains để truyền hàm isLong vào filter. Thay vì làm vậy, ta có thể dùng lambda:

numLongChains :: Int
numLongChains = length (filter (\xs -> length xs > 15) (map chain [1..100]))

Lambda là biểu thức nên có thể truyền nó theo cách trên. Biểu thức (\xs -> length xs > 15) trả về một hàm, hàm này cho ta biết rằng chiều dài List được truyền vào có hơn 15 hay không.

Những người chưa quen với cách hoạt động của curry và áp dụng từng phần thì hay dùng lambda nhưng lại thừa thải. Chẳng hạn, map (+3) [1,6,3,2] và map (\x -> x + 3) [1,6,3,2] tương đương vì (+3) và \x -> x + 3 đều trả về tổng một số với 3. Cũng như hàm , lambda có thể nhận vào bất kì tham số nào:

ghci> zipWith (\a b -> (a * 30 + 3) / b) [5,4,3,2,1] [1,2,3,4,5]
[153.0,61.5,31.0,15.75,6.6]

Và cũng giống hàm, bạn có thể xài pattern matching với lambda. Khác biệt duy nhất là không thể định nghĩa nhiều pattern cho một tham số, chẳng hạn khiến cho các pattern [] và (x:xs) cùng chung tham số và rồi duyệt qua chúng. Nếu một lần match thất bại trong lambda thì sẽ quăng ra run time error, vì vậy phải cẩn thận khi pattern matching bằng lambda!

ghci> map (\(a,b) -> a + b) [(1,2),(3,5),(6,3),(2,6),(2,5)]
[3,8,9,8,7]

Thông thường lambda được bao bởi cặp ngoặc tròn, trừ khi chúng ta muốn chúng kéo dài hết dòng. Sau đây là một chi tiết thú vị: do các hàm được curry theo mặc định, hai điều sau là tương đương

addThree :: (Num a) => a -> a -> a -> a
addThree x y z = x + y + z
addThree :: (Num a) => a -> a -> a -> a
addThree = \x -> \y -> \z -> x + y + z

Nếu ta định nghĩa một hàm như thế này, sẽ dễ thấy được tại sao type signature lại như vậy. Có ba dấu -> trong cả type signature và định nghĩa hàm. Nhưng dĩ nhiên, cách viết hàm thứ nhất dễ đọc hơn, cách thứ hai chỉ là một mẹo để minh họa tính curry.

Tuy nhiên, cũng có lúc dùng cách viết này lại hay. Tôi nghĩ rằng hàm flip sẽ dễ đọc hơn khi ta định nghĩa như sau:

flip' :: (a -> b -> c) -> b -> a -> c
flip' f = \x y -> f y x

Mặc dù như vậy cũng giống với flip' f x y = f y x, ta đã làm rõ rằng, trong tuyệt đại đa số trường hợp, việc dùng hàm này đều để tạo nên hàm mới. Trường hợp thông dụng nhất với flip là gọi nó như tham số của hàm rồi truyền hàm đầu ra vào map hoặc filter. Vì vậy hãy dùng lambda theo cách này khi bạn muốn hàm được viết phải rõ ràng để áp dụng từng phần và truyền đến hàm khác như tham số.

Fold

Quay lại với ý tưởng trong Haskell #4: Đệ quy, có một chủ đề xuyên suốt khi chúng ta áp dụng đệ quy trên List. Thông thường, ta có điều kiện biên với List rỗng. Ta đã có pattern x:xs, sau đó thao tác lên head và phần còn lại của List. Hóa ra đây là kiểu mẫu rất thông dụng, vì vậy một số hàm có kèm theo pattern này. Những hàm này có tên là fold. Chúng có cấu trúc như map, chỉ khác là rút gọn List thành một giá trị duy nhất.

Hàm fold nhận vào một hàm nhị phân, giá trị khởi tạo (tôi thích gọi là giá trị tích lũy) và List để fold. Hàm nhị phân này được truyền vào giá trị tích lũy và head (hoặc last), rồi tạo ra giá trị tích lũy mới. Sau đó, hàm nhị phân được gọi lại với giá trị tích lũy mới và head/last mới, và cứ như vậy. Một khi ta duyệt toàn bộ List, thì chỉ còn lại giá trị tích lũy, đó chính là giá trị mà List đã được rút gọn.

Trước hết, hãy xét hàm foldl, cũng được gọi là fold trái. Nó fold List từ phía trái. Hàm nhị phân được áp dụng giữa giá trị khởi tạo và head. Kết quả tạo ra giá trị tích lũy mới, và hàm nhị phân được gọi với giá trị mới đó và phần tử kế tiếp, …

Hàm sum có thể dùng fold thay vì đệ quy.

sum' :: (Num a) => [a] -> a
sum' xs = foldl (\acc x -> acc + x) 0 xs
Thử cái nào, một, hai, ba…:
ghci> sum' [3,5,2,1]
11

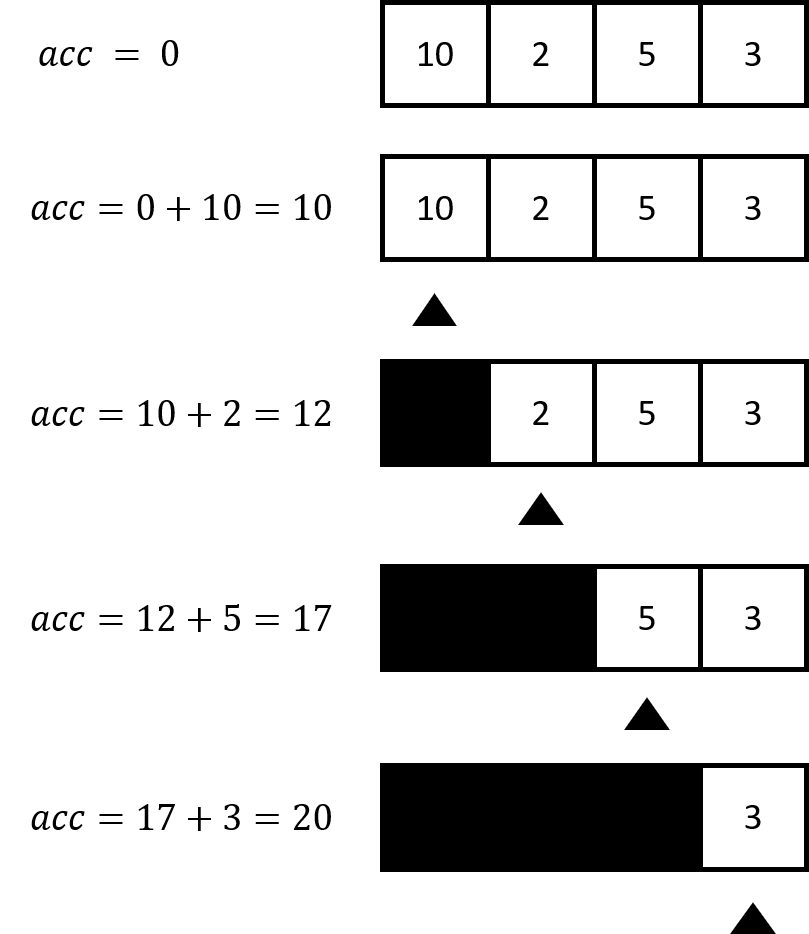
Ta hãy xét kĩ hơn cách làm việc của hàm fold. \acc x -> acc + x là hàm nhị phân. 0 là giá trị khởi tạo còn xs là List cần fold. Bây giờ, 0 được dùng làm tham số acc cho hàm nhị phân và 3 được dùng làm tham số x (hoặc phần tử hiện thời). 0 + 3 cho ra 3 và nó trở thành giá trị tích lũy mới. Tiếp theo, 3 được dùng làm giá trị tích lũy và 8 trở thành giá trị tích lũy mới. Tiếp tục, 8 là giá trị tích lũy, 2 là phần tử hiện thời, giá trị tích lũy mới sẽ là 10. Sau cùng, số 10 đó được dùng làm giá trị tích lũy và 1 là phần tử hiện thời, cho ra số 11. Xin chúc mừng, bạn đã fold xong!

Biểu đồ bên trên vẽ minh họa cho thấy từng bước quá trình fold xảy ra như thế nào. Bạn có thể thấy List kiểu như bị “gặm” hết từ phía bên trái giá trị tích lũy. Nếu sử dụng curry, ta còn có thể viết lại ngắn gọn hơn như sau:

sum' :: (Num a) => [a] -> a
sum' = foldl (+) 0

Hàm lambda (\acc x -> acc + x) cũng hệt như (+). Ta có thể bỏ qua xs là tham số vì việc gọi foldl (+) 0 sẽ trả về hàm nhận List. Nói chung, nếu bạn có hàm như foo a = bar b a, bạn có thể viết lại thành foo = bar b, vì tính curry.

Một ví dụ khác:

elem' :: (Eq a) => a -> [a] -> Bool
elem' y ys = foldl (\acc x -> if x == y then True else acc) False ys

Nào nào nào, ta đã làm gì vậy? Giá trị khởi tạo ở đây là kiểu boolean. Kiểu của giá trị tích lũy và kết quả luôn giống nhau khi ta thao tác với fold. Hãy nhớ rằng nếu bạn không biết rằng phải lấy giá trị khởi tạo là gì, thì điều trên sẽ gợi ý cho bạn. Ta xuất phát với False. Có lý khi dùng False làm giá trị khởi tạo. Giả sử rằng ta gọi fold đối với List rỗng, kết quả sẽ là giá trị khởi tạo. Sau đó ta kiểm tra phần tử hiện tại xem có phải là phần tử cần tìm không. Nếu đúng, ta đặt giá trị tích lũy là True. Nếu không, ta chỉ việc giữ nguyên giá trị tích lũy. Nếu trước đây nó là False, thì nó vẫn như vậy vì phần tử hiện thời không phải là thứ cần tìm. Nếu nó là True, thì ta cứ để như vậy.

Fold phải (foldr): hoạt động tương tự như fold trái, chỉ khác là List bị gặm dần từ phía phải. Ngoài ra, hàm nhị phân trong fold trái thì có giá trị tích lũy đứng làm tham số thứ nhất và giá trị hiện thời làm tham số thứ hai (\acc x -> ...), còn hàm nhị phân trong fold phải có giá trị hiện thời làm tham số thứ nhất và giá trị tích lũy làm tham số thứ hai (\x acc -> ...). Có lý khi nhận thấy rằng hàm fold phải có giá trị tích lũy bên phải, vì nó thực thi fold từ đó.

Giá trị fold của hàm fold có thể thuộc kiểu bất kì. Nó có thể là number, boolean, thậm chí là List mới. Ta sẽ tạo hàm map bằng fold phải. Giá trị tích lũy sẽ là một List, ta sẽ map từng phần tử một. Theo đó, hiển nhiên phần tử đầu tiên phải là List rỗng.

map' :: (a -> b) -> [a] -> [b]
map' f xs = foldr (\x acc -> f x : acc) [] xs

Nếu ta map (+3) lên [1,2,3], ta sẽ map List từ phía bên phải. Ta lấy phần tử cuối cùng, 3 rồi áp dụng hàm cho nó, kết quả là 6. Sau đó, ta nối kết quả này vào giá trị tích lũy, []. Bây giờ 6:[] bằng [6] và đây là giá trị tích lũy mới. Ta áp dụng (+3) cho 2, nó bằng 5, vì vậy giá trị tích lũy mới sẽ là [5,6]. Ta áp dụng (+3) đối với 1 rồi đặt trước nó với giá trị tích lũy và vì vậy giá trị cuối cùng là [4,5,6].

Dĩ nhiên, ta có thể cũng đã áp dụng hàm này với foldl. Khi đó sẽ là map' f xs = foldl (\acc x -> acc ++ [f x]) [] xs, nhưng vấn đề là ++ lại tốn thời gian hơn nhiều so với :, vì vậy ta sẽ dùng foldr khi map các List mới từ List cũ.

Nếu cần đảo ngược một List, bạn có thể foldr giống như đã làm với foldl và ngược lại. Thậm chí đôi khi bạn còn không phải làm như thế. Hàm sum có thể foldl hoặc foldr đều khá giống nhau. Một điểm khác biệt lớn là fold phải hoạt động được với các List vô hạn, còn foldl thì không! Nói thẳng ra, nếu bạn lấy List vô hạn từ một điểm nào đó rồi fold bên phải, cuối cùng bạn sẽ đến được đầu trái. Nhưng nếu lấy List vô hạn tại điểm nào đó rồi fold trái thì sẽ không bao giờ kết thúc!

Fold có thể được dùng để thực thi bất kì hàm duyệt List nào, từng phần tử một, rồi trả về thứ gì đó dựa vào việc duyệt. Mỗi khi bạn muốn duyệt List để trả về một thứ, thì nhiều khả năng là bạn muốn dùng một hàm fold. Đó là lý do tại sao, bên cạnh map và filter, fold là một trong những hàm hữu dụng nhất trong lập trình hàm.

Các hàm foldl1 và foldr1 cũng hoạt động giống như foldl và foldr, chỉ khác là bạn không cần cung cấp cho chúng giá trị khởi tạo cụ thể. Chúng sẽ giả sử phần tử đầu (hoặc cuối) của List làm giá trị khởi tạo rồi bắt đầu việc fold với phần tử kế. Lưu ý điều này, ta có thể viết hàm sum như sau: sum = foldl1 (+). Vì chúng phụ thuộc vào các List phải có ít nhất là một phần tử, nên sẽ có run time error nếu gọi chúng với List rỗng. Nhưng foldl và foldr lại chạy được với List rỗng. Khi bạn xài fold, hãy hình dung hàm sẽ hoạt động ra sao với List rỗng. Nếu hàm vô nghĩa khi truyền vào List rỗng, thì bạn có thể dùng foldl1 và foldr1.

Để thấy sức mạnh của fold, ta sẽ thực thi lại những hàm trong thư viện chuẩn:

maximum' :: (Ord a) => [a] -> a
maximum' = foldr1 (\x acc -> if x > acc then x else acc)

reverse' :: [a] -> [a]
reverse' = foldl (\acc x -> x : acc) []

product' :: (Num a) => [a] -> a
product' = foldr1 (*)

filter' :: (a -> Bool) -> [a] -> [a]
filter' p = foldr (\x acc -> if p x then x : acc else acc) []

head' :: [a] -> a
head' = foldr1 (\x _ -> x)

last' :: [a] -> a
last' = foldl1 (\_ x -> x)

Dùng pattern matching để code hàm head sẽ tốt hơn, nhưng trên đây chỉ nhằm giới thiệu cho thấy bạn có thể code bằng fold. Tôi nghĩ rằng định nghĩa reverse’ khá khéo léo. Ta lấy giá trị khởi tạo là List rỗng rồi tiếp cận List từ bên trái và chỉ việc đặt nó trước giá trị tích lũy. Cuối cùng, ta có được List đảo ngược. \acc x -> x : acc trông giống như kiểu hàm : chỉ khác là các tham số được đảo ngược. Đó là lý do tại sao ta đã có thể viết flip dưới dạng foldl (flip (:)) [].

Một cách khác để hình dùng hàm foldl và foldr như sau: chẳng hạn ta fold với hàm nhị phân $f$ cùng giá trị khới đầu $z$. Nếu ta foldr List [3,4,5,6], thực chất là ta làm như sau: f 3 (f 4 (f 5 (f 6 z))). $f$ được gọi với last List và giá trị tích lũy, giá trị đó lại đóng vai trò là giá trị tích lũy với giá trị áp chót, và cứ như vậy. Nếu ta chọn $f$ là $+$ và giá trị tích lũy khởi tạo là 0, thì kết quả sẽ là 3 + (4 + (5 + (6 + 0))). Hoặc nếu ta viết + dưới dạng hàm tiền tố, nó sẽ là (+) 3 ((+) 4 ((+) 5 ((+) 6 0))). Tương tự, thực thi foldl đối với List bằng hàm nhị phân $g$ và giá trị tích lũy $z$ sẽ tương đương với g (g (g (g z 3) 4) 5) 6. Nếu ta dùng flip (:) làm hàm nhị phân và [] làm giá trị tích lũy (để đảo ngược List), thì nó sẽ tương đương với flip (:) (flip (:) (flip (:) (flip (:) [] 3) 4) 5) 6. Và chắc hẳn, bạn sẽ thu được [6,5,4,3].

scanl và scanr cũng như foldl và foldr, chỉ khác là chúng xuất ra những trạng thái trung gian của giá trị tích lũy dưới dạng List. Cũng có scanl1 và scanr1, vốn tương tự như foldl1 và foldr1.

ghci> scanl (+) 0 [3,5,2,1]
[0,3,8,10,11]

ghci> scanr (+) 0 [3,5,2,1]
[11,8,3,1,0]

ghci> scanl1 (\acc x -> if x > acc then x else acc) [3,4,5,3,7,9,2,1]
[3,4,5,5,7,9,9,9]

ghci> scanl (flip (:)) [] [3,2,1]
[[],[3],[2,3],[1,2,3]]

Khi dùng scanl, kết quả sau cùng sẽ là last List, còn scanr sẽ đặt kết quả lên head List.

Scan được dùng để theo dõi tiến trình của hàm thực thi. Hãy trả lời câu hỏi này: Cần lấy bao nhiêu phần tử để tạo nên tổng của các căn bậc hai các số nguyên sao cho tổng này vượt quá 1000? Để lấy căn bậc hai của số tự nhiên, ta chỉ cần viết map sqrt [1..]. Bây giờ để lấy tổng, ta có thể fold, nhưng vì ta quan tâm đến việc tổng này diễn biến ra sao, nên ta sẽ scan. Khi scan xong, ta sẽ thấy được có bao nhiêu tổng nhỏ hơn 1000. Bình thường thì tổng thứ nhất trong List scan bằng 1. Tổng thứ hai sẽ bằng 1 cộng với căn [bậc hai] của 2. Tổng thứ ba thì bằng lượng đó cộng với căn của 3. Nếu có X tổng dưới 1000, thì sẽ có X+1 phần tử cần để tổng vượt 1000.

sqrtSums :: Int
sqrtSums = length (takeWhile (<1000) (scanl1 (+) (map sqrt [1..]))) + 1
ghci> sqrtSums
131
ghci> sum (map sqrt [1..131])
1005.0942035344083
ghci> sum (map sqrt [1..130])
993.6486803921487

Ở đây ta dùng takeWhile thay vì filter bởi lẽ filter không làm việc với List vô hạn. Ngay cả khi ta biết rằng List giảm dần, filter cũng không biết, vì vậy dùng takeWhile để cắt List ở chỗ xuất hiện tổng lớn hơn 1000.

$

Được rồi, tiếp theo ta sẽ xét đến hàm $, còn được gọi là áp dụng hàm. Trước hết, hãy kiểm tra xem nó được định nghĩa thế nào:

($) :: (a -> b) -> a -> b
f $ x = f x

Gì thế này? Cái toán tử vô dụng này là gì? Đó chỉ là việc áp dụng hàm! À, gần đúng như vậy, nhưng không hẳn! Nếu như áp dụng hàm thông thường (đặt một dấu cách giữa hai thứ) có độ ưu tiên rất cao, thì $ lại có độ ưu tiên thấp nhất. Việc áp dụng hàm bằng dấu cách thì có tính kết trái (theo đó f a b c tương đương ((f a) b) c)), còn áp dụng hàm với $ lại có tính kết phải.

Nghe vậy cũng ổn, nhưng điều đó giúp được gì cho ta? Trong hầu hết các tình huống, đó là một hàm rất tiện để đỡ viết dấu ngoặc tròn. Xét biểu thức sum (map sqrt [1..130]). Vì $ có độ ưu tiên thấp nên ta có thể viết lại biểu thức như sau: sum $ map sqrt [1..130], và đã tiết kiệm được những lần gõ phím quý giá! Khi gặp dấu $, biểu thức bên tay phải $ sẽ là tham số cho hàm bên trái. Thế còn sqrt 3 + 4 + 9 thì sao? Ở đây 9, 4 và $\sqrt{3}$ được cộng lại với nhau. Nếu muốn tính $\sqrt{3 + 4 + 9}$, ta phải viết sqrt (3 + 4 + 9) hoặc nếu dùng $, thì có thể viết sqrt $ 3 + 4 + 9 vì $ có độ ưu tiên thấp nhất. Đó là lý do bạn có thể hình dùng dấu $ tương đương với dấu mở ngoặc tròn và đóng ngoặc tròn nữa về hết phía bên phải của biểu thức.

Thế còn sum (filter (> 10) (map (*2) [2..10]))? À, vì $ có tính kết hợp phải, nên f (g (z x)) thì bằng với f $ g $ z x. Và do đó, ta có thể viết sum (filter (> 10) (map (*2) [2..10])) thành sum $ filter (> 10) $ map (*2) [2..10].

Ngoài việc bỏ bớt cặp ngoặc tròn, $ còn mang ý nghĩa sâu xa rằng “áp dụng hàm” chính là hàm. Bằng cách này, ta có thể map hàm “áp dụng hàm” với List các hàm.

ghci> map ($ 3) [(4+), (10*), (^2), sqrt]
[7.0,30.0,9.0,1.7320508075688772]

Kết thúc bài 6

Haskell #7: Hàm hợp